I am so upset
 

I just went to take an online exam in my forensics class. This class is very hard but I started the exam and was doing quite well until it got stuck loading between pages. I'd only done about 10 out of 44 questions. I sat there for more than 10 minutes waiting and waiting and finally thought perhaps I could reload the page. Big mistake...it locked me out of the exam. So now I'm waiting to hear back from the professor to see if there's any way I can get back in. I sat there just yelling "fvck fvck fvk" over and over after I locked myself out. I am so upset I could just cry.
:crying:

Re: I am so upset
 

as it is an online test, i am sure the professor has encountered similiar stories before....its not like you exited early to cheat the system...it will be alright....

Re: I am so upset
 

That sucks.

Re: I am so upset
 

Hang in there. Your not the only one! Testing this way is problematic and in many cases unproven. It would be interesting to know the reliability factor vs the anxiety results for this method of test.:mad: :violin: :confused:

Re: I am so upset
 

Sux and sorry to hear, but it sounds like you had a connectivity problem and when you refreshed the page your IP had changed thus causing the lock out as it thought someone else was trying to access your test from a diffrent source...

Welcome to the world of technology.... aint it great?

Re: I am so upset
 

I got back in. One of the teacher/students unlocked me and I'm almost done. I'm just waiting on some help with a probability question. Questions like this:
You are a professor making up a 4-answer multiple-choice question pool for a test. You make up 20 questions and distribute the four options for answers equally among the questions. You want four questions from the pool to be inserted randomly into your test. In how many ways will you get all of the questions having the same option as the answer?
I hate math questions! Thank you all for your sympathy...I was so very upset even though I knew it'd probably work out.

Re: I am so upset
 

Factorials and permutations:

The factorial function is formally defined by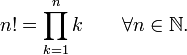
The above definition incorporates the instance
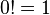as an instance of the fact that the product of no numbers at all is 1. This fact for factorials is useful, because

• the recursive relation works for n = 0;
• this definition makes many identities in combinatorics valid for zero sizes.
  • In particular, the number of combinations or permutations of an empty set is, clearly, 1.

Applications

• Factorials are used in combinatorics. For example, there are n! different ways of arranging n distinct objects in a sequence. (The arrangements are called permutations.) And the number of ways one can choose k objects from among a given set of n objects (the number of combinations), is given by the so-called binomial coefficient

• In permutations, if r objects can be chosen and arranged in r different ways from a total of n objects, where r ≤ n, then the total number of distinct permutations is given by:

Re: I am so upset
 

WTF is that stuff! LOL Math is not my forte, I mean I'm like the Forrest Gump of math. Seriously!

Re: I am so upset
 

Run Forest, Run!

Re: I am so upset
 

Fixed:jump:

Re: I am so upset
 

ROFL!!

Re: I am so upset
 

Glad you like it. That's going to be your avatar.:clapping:

Re: I am so upset
 

You are full of it...

n = +- the sum of (n2-n / n2 - N sq) - r2/Pr (K) minus the root of k3+k (0) assuming t 8th is = negative............

Re: I am so upset
 

3...

Re: I am so upset
 

Products and ordering, how blase'.