Quote:
|
Originally Posted by Karsun
You are a professor making up a 4-answer multiple-choice question pool for a test. You make up 20 questions and distribute the four options for answers equally among the questions. You want four questions from the pool to be inserted randomly into your test. In how many ways will you get all of the questions having the same option as the answer?
|
Factorials and permutations:
The factorial function is formally defined by
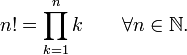
The above definition incorporates the instance
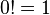
as an instance of the fact that the
product of no numbers at all is 1. This fact for factorials is useful, because
- the recursive relation
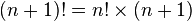works for n = 0; - this definition makes many identities in combinatorics valid for zero sizes.
- In particular, the number of combinations or permutations of an empty set is, clearly, 1.
Applications
- Factorials are used in combinatorics. For example, there are n! different ways of arranging n distinct objects in a sequence. (The arrangements are called permutations.) And the number of ways one can choose k objects from among a given set of n objects (the number of combinations), is given by the so-called binomial coefficient
- In permutations, if r objects can be chosen and arranged in r different ways from a total of n objects, where r ≤ n, then the total number of distinct permutations is given by:
